ycleEnRISLANCOIRfsystemutrintrintln

Planche 1

Inf 431 -- Cours 2
Dags -- Connexité 1
http://jeanjacqueslevy.net
secrétariat de l'enseignement:
Catherine Bensoussan
cb@lix.polytechnique.fr
Aile 00, LIX,
01 69 33 34 67
http://www.enseignement.polytechnique.fr/informatique/IF

Planche 2

Délégués

.5@percent

Deux délégués pour IF 431
Délégués PC/TD

Plan

.5@percent

Arbres de recouvrement
Détection de cycles
Tri topologique
Composantes connexes
Bi-connexité et points d'articulation

Planche 3

Rappel sur les listes

aluivant

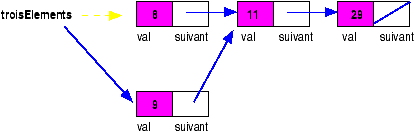
int val; Liste suivant; Listes d'entiers Liste (int x, Liste s) { val = x; suivant = s; }} class X { static Liste listeVide = null; public static void main (String[ ] args) { Liste troisElements = new Liste(8, new Liste(2, new Liste(29, null))); troisElements.suivant.val = 11; System.out.println (troisElements.suivant.suivant.val); troisElements = new Liste (9, troisElements.suivant);} }

Planche 4

Parcours en profondeur (1/2)

static numOrdre;static void visiter (Graphe g) { int n = g.succ.length; int[ ] couleur = new int[n]; numOrdre = -1; for (int x = 0; x < n; ++x) num[x] = -1; for (int x = 0; x < n; ++x) couleur[x] = BLANC; for (int x = 0; x < n; ++x) if (couleur[x] == BLANC) dfs(g, x, couleur, num);}static void dfs (Graphe g, int x, int[ ] couleur, int[ ] num) { couleur[x] = GRIS; num[x] = ++numOrdre; Pour tout y successeur de x dans G faire { if (couleur[y] == BLANC) dfs(g, y, couleur, num); } couleur[x] = NOIR;}

Planche 5

Parcours en profondeur (2/2)

static numOrdre;static void visiter (Graphe g) { int n = g.succ.length; int[ ] couleur = new int[n]; numOrdre = -1; for (int x = 0; x < n; ++x) num[x] = -1; for (int x = 0; x < n; ++x) couleur[x] = BLANC; for (int x = 0; x < n; ++x) if (couleur[x] == BLANC) dfs(g, x, couleur, num);}static void dfs (Graphe g, int x, int[ ] couleur, int[ ] num) { couleur[x] = GRIS; num[x] = ++numOrdre; for (Liste ls = g.succ[x]; ls != null; ls = ls.suivant) { int y = ls.val; if (couleur[y] == BLANC) dfs(g, y, couleur, num); } couleur[x] = NOIR;}

Planche 6

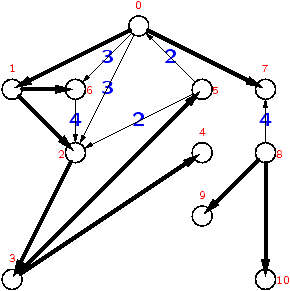
Sortie de labyrinthe

On cherche un chemin de x à s.

hemin

couleur[x] = GRIS; if (x == s) return new Liste (x, null); for (Liste ls = g.succ[x]; ls != null; ls = ls.suivant) { int y = ls.val; if (couleur[y] == BLANC) { Liste r = chemin (g, y, s); if (r != null) return new Liste (x, r); } } return null;}

chemin retourne la liste des sommets sur le chemin trouvé vers la sortie s.
Þ Ne pas oublier que la fonction dfs peut retourner un résultat.
Complexité en temps en O(V+E)

Planche 7

Arbres de recouvrement (1/4)

4 sortes d'arcs par rapport aux branches d'un arbre de recouvrement:

d'un noeud de l'arbre à un fils dans l'arbre
d'un noeud de l'arbre à un ancètre dans l'arbre
d'un noeud de l'arbre à un descendant non direct dans l'arbre
d'un noeud à un cousin dans l'arbre (forêt)

Planche 8

Arbres de recouvrement (2/4)

Mais, dans un graphe non-orienté, deux sortes d'arcs dans dfs:

Rappel: Dans notre représentation des graphes non-orientés, un arc coexiste avec son arc inverse; donc les cas 1-2, 3-2 coexistent.

Graphe non-orienté Þ pas d'arcs de type 4 º pas d'arcs transverses.

Planche 9

Arbres de recouvrement (3/4)

d(x) est le temps où x devient GRIS dans dfs
f(x) est le temps où x devient NOIR dans dfs

Proposition 1 [Intervalles parenthésés] Soient s et t deux sommets. Alors 3 cas seulement:

les intervalles [d(s), f(s)] et [d(t), f(t)] sont disjoints et
s et t sont cousins dans l'arbre de recouvrement;
l'intervalle [d(s), f(s)] contient [d(t), f(t)] et
s admet t comme descendant dans l'arbre de recouvrement;
l'intervalle [d(s), f(s)] est contenu dans [d(t), f(t)] et
s admet t comme ancêtre dans l'arbre de recouvrement;

Proposition 2 [Caractérisation par numéros] Soit e un arc de s à t. Alors:

e est de type 1 ou 3 ssi num[s] < num[t].
e est de type 2 ou 4 ssi num[s] > num[t].

Planche 10

Arbres de recouvrement (4/4)

Soit d(e) le temps où on considère l'arc e pour la première fois dans dfs.

Proposition 3 [Caractérisation par couleurs] Soit e un arc de s à t. Alors:

e est de type 1 ssi couleur[t] = BLANC au temps d(e).
e est de type 2 ssi couleur[t] = GRIS au temps d(e).
e est de type 3 ou 4 ssi couleur[t] = NOIR au temps d(e).

Un chemin blanc est un chemin dont tous les sommets intermédiaires sont BLANCs.

Proposition 4[Chemins blancs] Le sommet t est un descendant de s dans un arbre de recouvrement ssi il existe un chemin blanc de s GRIS vers t BLANC lors de l'exploration de s par le dfs correspondant.

Planche 11

Détection de cycles (1/3)



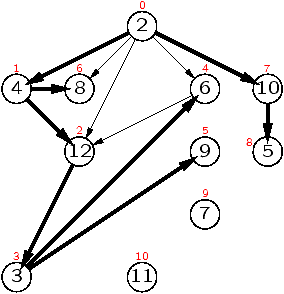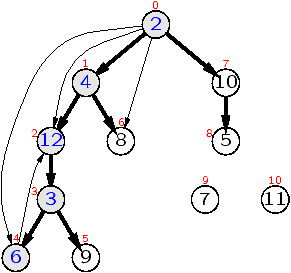graphe avec cycle		arbre de recouvrement

Cycle ss'il existe un arc de type 2 pendant la construction de l'arbre de recouvrement.

Planche 12

Détection de cycles (2/3)

Définition 5 Le point d'attache d'un cycle est le premier sommet du cycle visité par dfs.

Þ Le point d'attache est le sommet s du cycle dont num[s] est minimal.

Proposition 6 Le graphe est cyclique ss'il existe un arc e vers un sommet GRIS au temps d(e).

Démonstration

S'il existe un arc e de s à t GRIS au temps d(e), alors e est un arc de type 2. Il existe un cyle de t passant par s et revenant à t.
S'il existe un cycle de point d'attache t, au début de l'exploration du cycle le sommet t est GRIS, les autres sont BLANCs dans le cycle. Il existe un chemin blanc de t au prédécesseur t' de t dans le cycle. Donc t' est un descendant de t dans l'arbre de recouvrement. Et il existe un arc e de t' à t GRIS au temps d(e).

Planche 13

Détection de cycles (3/3)

final static int BLANC = 0, GRIS = 1, NOIR = 2;static boolean acyclique (Graphe g) { int n = g.succ.length; int[ ] couleur = new int[n]; for (int x=0; x < n; ++x) couleur[x] = BLANC; for (int x=0; x < n; ++x) if ( couleur[x] == BLANC && cycleEn(g, x, couleur) ) return false; return true;}static boolean cycleEn(Graphe g, int x, int[ ] couleur) { couleur[x] = GRIS; for (Liste ls = g.succ[x]; ls != null; ls = ls.suivant) { int y = ls.val; if ( couleur[y] == GRIS || couleur[y] == BLANC && cycleEn(g, y, couleur) ) return true; } couleur[x] = NOIR; return false;}

Planche 14

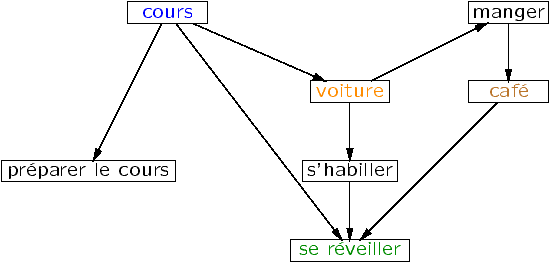
Tri topologique (1/4)

G=(V,E) est un graphe acyclique (dag: directed acyclic graph)

Donner une liste des sommets á v_i | i=1..nñ dans un ordre compatible avec l'ordre induit par G: v_i < v_j Û v_j ® v_i.

(trouver un ordre total compatible avec un ordre partiel donné)

Planche 15

Tri topologique (2/4)

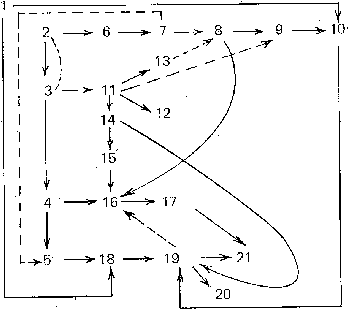Ordre de lecture

des chapîtres

du livre de

H. P. Barendregt

The l-calculus:

its syntax and semantics

North-Holland, 1980

Autre exemple: trouver l'ordre d'exécution des tâches d'un projet à partir du graphe de dépendances (ordonnancement).

Planche 16

Tri topologique (3/4)

Si le sommet terminal est connu, un parcours en profondeur suffit.

final static int BLANC = 0, GRIS = 1, NOIR = 2;static Liste aFaire (Graphe g, int x) { int n = g.succ.length; int[ ] couleur = new int[n]; for (int x = 0; x < n; ++x) couleur[x] = BLANC; return dfs(g, x, null, couleur);}static Liste dfs(Graphe g, int x, Liste r, int[ ] couleur) { couleur[x] = GRIS; for (Liste ls = g.succ[x]; ls != null; ls = ls.suivant) { int y = ls.val; if (couleur[y] == BLANC) r = dfs(g, y, r, couleur); } return new Liste (x, r);}

r est un accumulateur pour le résultat º liste des sommets à faire.

Planche 17

Tri topologique (4/4)

Pour trouver les sommets terminaux (dont aucun autre ne dépend), un parcours linéaire des arcs suffit.

erminal

static boolean[ ] calculerTerminaux (Graphe g) { int n = g.succ.length; int[ ] terminal = new boolean[n]; for (int x = 0; x < n; ++x) terminal[x] = true; for (int x = 0; x < n; ++x) for (Liste ls = g.succ[x]; ls != null; ls = ls.suivant) { int y = ls.val; terminal[y] = false; } return terminal;}

Complexité en O(V+E).

Autre algorithme [Knuth] sur le graphe inverse.

Planche 18

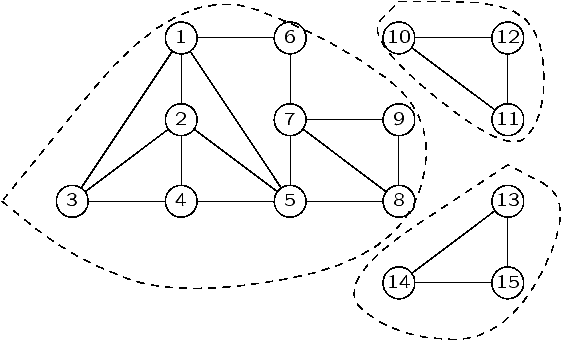
Connexité

Existe-t'il un chemin entre deux sommets?
(dfs; cf. sortie de labyrinthe). Complexité O(V+E).
Trouver l'ensemble des sommets accessibles depuis un sommet. (dfs). Complexité O(V+E).
Trouver les ensembles de sommets interconnectés dans un graphe non-orienté. Composantes connexes.
(cf. plus loin; dfs) Complexité O(V+E).
Même problème dans un graphe orienté? Composantes fortement connexes. (cf. plus loin; dfs) Complexité O(V+E).

Planche 19

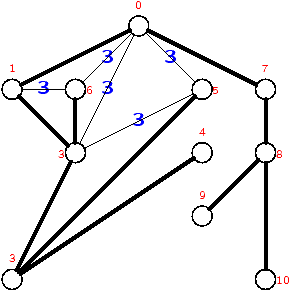
Composantes connexes (1/2)

Le graphe est non-orienté.

Planche 20

Composantes connexes (2/2)

mprimerComposanteDe

static void imprimerCompConnexes (Graphe g) { int n = g.succ.length; int[ ] couleur = new int[n]; for (int x = 0; x < n; ++x) couleur[x] = BLANC; for (int x = 0; x < n; ++x) { if (couleur[y] == BLANC) { imprimerComposanteDe(g, x, couleur); System.out.println();} } }static void imprimerComposanteDe(Graphe g, int x, int[ ] couleur) { couleur[x] = GRIS; System.out.print (x + " "); for (Liste ls = g.succ[x]; ls != null; ls = ls.suivant) { int y = ls.val; if (couleur[y] == BLANC) imprimerComposanteDe(g, y, couleur);} }

Exercice 1 Ecrire une fonction qui rend la liste des composantes connexes.

Planche 21

Bi-connexité (1/8)

Dans un graphe non-orienté, existe-t-il 2 chemins différents entre toute paire de noeuds?
Un point d'articulation est un point qui sépare le graphe en parties non connexes si on l'enlève.
Un graphe connexe sans point d'articulation est bi-connexe.
Exemples: les rues de Paris, la distribution d'électricité, la topologie d'un réseau informatique, etc. Il vaut mieux que ces graphes soient bi-connexes.

Planche 22

Bi-connexité (2/8)

Le point d'attache de x est le sommet t avec le plus petit num[t] tel qu'un chemin relie x à t avec au plus un seul arc de retour.

Planche 23

Bi-connexité (3/8)

Définition 7 Un circuit est un chemin formé par les arcs e₁, e₂, ...e_n (n ³ 0) tels que:

ext(e_i) = org(e_i+1) pour 1 £ i < n
ext(e_n) = org(e₁)

Définition 8 Un circuit élémentaire est un chemin dont tous les sommets sont distincts (à l'exception du premier et du dernier).

Proposition 9 Le point d'attache de x est le point d'attache t de numéro num[t] minimum parmi tous les circuits élémentaires passant par x.

Planche 24

Bi-connexité (4/8)

Vue de l'arbre de recouvrement

Un point d'articulation x a un descendant direct y dont le point d'attache t vérifie num[x] ³ num[t]. Par exemple: x Î {3, 10, 2}

ttachettache1

Planche 25

Bi-connexité (5/8)

Calcul (en dfs) du numéro de parcours du point d'attache de x.

static int attache(Graphe g, int x) { int min = num[x] = ++numOrdre; for (Liste ls = g.succ[x]; ls != null; ls = ls.suivant) { int y = ls.val; int m; if (num[y] == -1) { m = attache(g, y); if (m >= num[x]) articulation[x] = true; } else m = num[y]; min = Math.min (min, m); } return min;}

2244

Planche 26

Bi-connexité (6/8)

Avec le critère précédent, tout sommet à la racine de l'arbre de recouvrement serait un point d'articulation.

Correction: le sommet à la racine de l'arbre de recouvrement est un point d'articulation ssi ce sommet a plus qu'un fils dans l'arbre.

static int numOrdre; static int[ ] num;static boolean[ ] articulation;static void trouverArticulations (Graphe g) { int n = g.succ.length; num = new int[n]; numOrdre = -1; articulation = new boolean[n]; for (int x = 0; x < n; ++x) { num[x] = -1; articulation[x] = false; } for (int x = 0; x < n; ++x) if (num[x] == -1) { attache1(g, x); }}

Planche 27

Bi-connexité (7/8)

static void attache1(Graphe g, int x) { num[x] = ++numOrdre; int nfils = 0; for (Liste ls = g.succ[x]; ls != null; ls = ls.suivant) { int y = ls.val; if (num[y] == -1) { ++nfils; attache(g, y); } } articulation[x] = nfils > 1;}

On peut déplier cette fonction (inlining) dans trouverArticulations.

Planche 28

Bi-connexité (8/8)

static void trouverArticulations (Graphe g) { int n = g.succ.length; numOrdre = -1; num = new int[n]; articulation = new boolean[n]; for (int x = 0; x < n; ++x) { num[x] = -1; articulation[x] = false; } for (int x = 0; x < n; ++x) if (num[x] == -1) { num[x] = ++numOrdre; int nfils = 0; for (Liste ls = g.succ[x]; ls != null; ls = ls.suivant) { int y = ls.val; if (num[y] == -1) { ++nfils; attache(g, y); } } articulation[x] = nfils > 1; }}

Complexité en O(V+E).

Planche 29

Exercices

Exercice 2 Ecrire trouverArticulations sans variables globales.

Exercice 3 Ecrire un programme qui teste la bi-connexité d'un graphe.

Exercice 4 (difficile) Ecrire un programme qui imprime les composantes bi-connexes.

Exercice 5 Définir la notion de composante tri-connexe.

Exercice 6 La commande make du système Unix fait une analyse de dépendances pour reconstruire un projet informatique. Réfléchir à sa programmation. Certaines versions permettent la reconstruction parallèle où plusieurs commandes peuvent s'exécuter en parallèle sur p processeurs. Comment adapter l'analyse de dépendances?

This document was translated from L^AT_EX by H^EV^EA.