Planche 1

Inf 431 -- Cours 4
 Exploration


Non déterminisme
http://jeanjacqueslevy.net
secrétariat de l'enseignement:
Catherine Bensoussan
cb@lix.polytechnique.fr
Aile 00, LIX,
01 69 33 34 67
 http://www.enseignement.polytechnique.fr/informatique/IF

Planche 2

Plan


.65@percent
  1. Backtracking
  2. Algorithmes gloutons
  3. Programmation dynamique
  4. Enumération brutale

[D. Harel], Algorithmics: The Spirit of Computing, Addison-Wesley, 1st edition, 1987; 2nd edition, 1992; 3rd edition (with Y. Feldman), 2004.

Planche 3

Dominos de Wang (1/2)


p=4
n=6
 
4096
solutions

Pavages de carrés n× n avec p dominos (carrés à bords colorés).

Planche 4

Dominos de Wang (2/2)


p=3
n=6
 
3
solutions

Wang ® Berger ® Penrose

Planche 5

Les 8 reines (1/3)



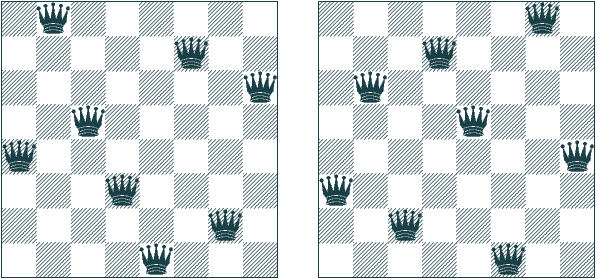
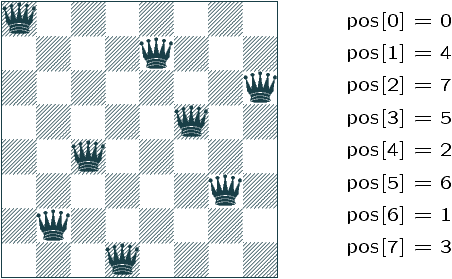
Mettre 8 reines sur un échiquier sans qu'elles ne soient en prise.

Planche 6

Les 8 reines (2/3)



pos[i] = j si la reine de la ligne i est en colonne j.

Planche 7

Les 8 reines (3/3)

Reineseinesonflitompatible
static void nReines (int n) {
  int[ ] pos = new int[n];  reines (pos, 0);
}

static void reines (int[ ] pos, int i) {
  if (i >= pos.length) imprimerEchiquier(pos);
  else
    for (int j = 0; j < pos.length; ++j)          // backtracking
      if (compatible (pos, i, j)) {
        pos[i] = j;
        reines (pos, i+1);
}     }

static boolean compatible (int[ ] pos, int i, int j) {
  for (int k = 0; k < i; ++k)
    if (conflit (i, j, k, pos[k])) return false;
  return true;
}

static boolean conflit (int i1, int j1, int i2, int j2) {
  return (i1 == i2) || (j1 == j2) ||
         (Math.abs (i1 - i2) == Math.abs (j1 - j2));
}

Planche 8

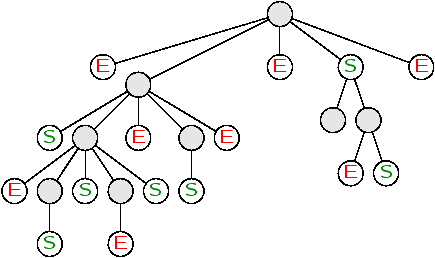
Backtracking (1/2)

Planche 9

Backtracking (2/2)

Exercice 1 Donner la complexité non déterministe des dominos de Wang.

Exercice 2 Donner la complexité non déterministe du problème des n reines.

Planche 10

Problèmes NP

La plus grande conjecture de l'informatique = un des 7 problèmes ouverts du millénaire en mathématiques (selon le Clay Institute):
P =? NP
     
déterministe
polynomial
=?
non déterministe
polynomial

[Cook, 1971]

Exemples de problèmes NP: satisfiabilité des expressions booléennes, 3SAT (satisfiabilité des expressions booléennes en forme normale conjonctive avec 3 variables), isomorphisme de sous-graphes, couverture de graphes, circuits hamiltoniens, voyageur de commerce, sac à dos, etc. [Karp, 1972]

cf. le cours Conception et Analyse des algorithmes en Majeure 2.

Planche 11

3 stratégies d'exploration

avalierbCoupsDeIBREansEchiquier
Planche 12

Cavalier d'Euler (1/2)

Un cavalier doit parcourir toutes les cases d'un échiquier sans passer deux fois par la même case. Algorithme: aller vers la case où on peut le moins se déplacer, le coup suivant.
final static int LIBRE = -1;
final static int[ ] x = {2, 1, -1, -2, -2, -1,  1,  2};
final static int[ ] y = {1, 2,  2,  1, -1, -2, -2, -1};

static void cavalier (int[ ][ ] m, int i, int j) {
  int coup = 0; int i0, j0;
  do {
    m[i][j] = coup++;
    i0 = i; j0 = j;
    int min = Integer.MAX_VALUE;
    for (int k = 0; k < x.length; ++k) {
      int n = nbCoupsDe (m, i0+x[k], j0+y[k]);
      if (min > n) {
        i = i0+x[k]; j = j0+y[k];
        min = n;
    } }
  } while (i != i0 || j != j0);
}
Planche 13

Cavalier d'Euler (2/2)


static int nbCoupsDe (int[ ][ ] m, int i, int j) {
  if ( !dansEchiquier (m, i, j) || m[i][j] != LIBRE )
    return Integer.MAX_VALUE;
  else {
    int res = 0;
    for (int k = 0; k < x.length; ++k) {
      int i1 = i+x[k], j1 = j+y[k];
      if ( dansEchiquier (m, i1, j1) && m[i1][j1] == LIBRE )
        ++res;
    }
    return res;
} }

static boolean dansEchiquier(int[ ][ ] m, int i, int j) {
  return 0 <= i && i < m.length && 0 <= j && j < m[0].length;
}

Exemple d'algorithme glouton.

Exercice 3 Montrer que cet algorithme marche pour toutes les cases de départ sauf une.

Planche 14

Programmation dynamique (1/2)

Planche 15

Programmation dynamique (2/2)

La fonction de [Fibonacci]
  if (n < 2) return n; else return fib (n-2) + fib (n-1);
}

se calcule plus rapidement en tabulant:
  int[ ] tab = new int[n+1];
  tab[0] = 0; tab[1] = 1;
  for (int i = 2; i <= n; ++i)
    tab[i] = tab[i-2] + tab[i-1];
  return tab[n];
}

(On peut même ne garder que les deux dernières valeurs!)

C'est un bel exemple de programmation dynamique.

lusLongueSSCINORD_OUESTUESTORDongueurred
Planche 16

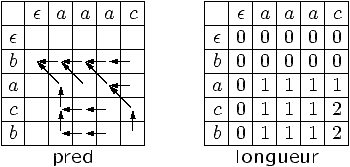
Plus longue sous-séquence commune (1/2)

Plus longue sous-séquence commune entre deux chaînes de caractères u, v Î S* (e chaîne vide).
FIN ssc(u, e) = ssc(e, u) = e
NORD_OUEST ssc(ua, va) = ssc(u,v)a
OUEST
NORD
ssc(ua, vb) =
ì
í
î
ssc(ua, v) si || ssc(ua, v)|| ³ || ssc(u, vb)||
ssc(u, vb) sinon

Commande Unix diff; séquençage de l'ADN

Planche 17

Plus longue sous-séquence commune (2/2)


final static int FIN = 0, NORD_OUEST = 1, OUEST = 2, NORD = 3;

static int[ ][ ] plusLongueSSC (String u, String v) {
  int m = u.length(); int n = v.length();
  int[ ][ ] longueur = new int[m][n], pred = new int[m][n];
  for (int i = 0; i < m+1; ++i) {longueur[i][0] = 0; pred[i][0] = FIN; }
  for (int j = 0; j < n+1; ++j) {longueur[0][j] = 0; pred[0][j] = FIN; } 

  for (int i = 1; i < m+1; ++i)
    for (int j = 1; j < n+1; ++j)
      if (u.charAt(i-1) == v.charAt(j-1)) {
        longueur[i][j] = 1 + longueur[i-1][j-1]; pred[i][j] = NORD_OUEST;
      } else if (longueur[i][j-1] >= longueur[i-1][j]) {
        longueur[i][j] = longueur[i][j-1]; pred[i][j] = OUEST;
      } else {
        longueur[i][j] = longueur[i-1][j]; pred[i][j] = NORD;
      }
   return pred;
}

Planche 18

Enumération de chemins (1/2)

Enumérer les chemins élémentaires dans un graphe (jamais deux fois un même sommet). ousLesCheminsDeRISLANCOIRfsystemutrintln
final static int BLANC = 0, GRIS = 1, NOIR = 2;

static void tousLesChemins (Graphe g) {
  int n = g.succ.length; int[ ] couleur = new int[n];
  for (int x=0; x < n; ++x) couleur[x] = BLANC;
  for (int x=0; x < n; ++x) tousLesCheminsDe (g, x, couleur, null);
}

static void tousLesCheminsDe (Graphe g, int x, int[ ] couleur, Liste c) {
  couleur[x] = GRIS;
  c = new Liste (x, c); System.out.println (c);
  for (Liste ls = g.succ[x]; ls != null; ls = ls.suivant) {
    int y = ls.val;
    if (couleur[y] != GRIS)
      tousLesCheminsDe (g, y, couleur, c);
  }
  couleur[x] = BLANC; // ¬ Le changement
}
Planche 19

Enumération de chemins (2/2)

ousLesCheminsDeoStringiste
class Liste {
  int val; Liste suivant;
  Liste (int v, Liste x) {val = v; suivant = x; }

  public String toString() {
    if (suivant == null) return "" + val;
    else return "" + suivant + " " + val ;
  }
}

On peut aussi écrire
  public String toString() {
    return (suivant == null ? "" : suivant + " ") + val ;

Affaire de goût!!
Enumération des chemins simples
=
légère modification sur dfs.

Planche 20

Exercices

Exercice 4 Enumérer les chemins simples en largeur d'abord.

Exercice 5 Tester si un graphe contient un circuit hamiltonien. (Circuit passant par tous les sommets sans passer 2 fois par le même).

Exercice 6 Même question dans un graphe non dirigé.

Exercice 7 Un tour de Euler dans un graphe dirigé consiste à passer par tous les arcs d'un graphe en ne passant jamais deux fois par le même arc. Ecrire un programme pour tester l'existence d'un tel tour.

Exercice 8 Même problème dans un graphe non dirigé.

Exercice 9 Complexité de SSC?

Exercice 10 Comment implémenter la commande diff du système Unix?

Exercice 11 L'associativité de la multiplication de matrices permet de multiplier n matrices M0M1... Mn-1 sans préciser le parenthésage. Pourtant, cela peut faire varier le nombre de multiplications scalaires à effectuer. Donner un algorithme qui utilise la programmation dynamique pour trouver l'ordre optimal.

This document was translated from LATEX by HEVEA.