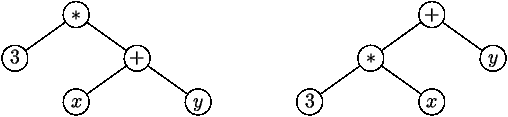Planche 1

Inf 431 -- Cours 6
Analyse syntaxique
http://jeanjacqueslevy.net
secrétariat de l'enseignement:
Catherine Bensoussan
cb@lix.polytechnique.fr
Aile 00, LIX,
01 69 33 34 67
http://www.enseignement.polytechnique.fr/informatique/IF

Planche 2

Plan

=8em Arbres de syntaxe abstraite (arbres binaires, termes)
Grammaires formelles
BNF
Arbres syntaxiques
Analyse récursive descendante
Evaluation d'expressions arithmétiques
Associativité

cf. les cours Automates et Calculabilité en majeure M1 pour les grammaires formelles, et Compilation en majeure M2 pour les analyseurs syntaxiques

Planche 3

Schéma général

Texte
ß

Analyse lexicale

ß
Flot de lexèmes
ß

Analyse syntaxique

ß
Arbre Syntaxe Abstraite (ASA)

Planche 4

Arbres de syntaxe abstraite

Le texte est non structuré
ASA = structure de donnée abstraite pour traiter un problème
Exemples de problèmes:
- ·lire/écrire des arbres binaires
- ·calculer des expressions arithmétiques
- ·interpréter un petit langage de commandes
- ·calculer symboliquement (algèbre, logique)
- ·générer du code machine (compilation)
Exemples d'ASAs:
- ·arbres binaires
- ·termes représentant une expression arithmétique

rbreerme

Planche 5

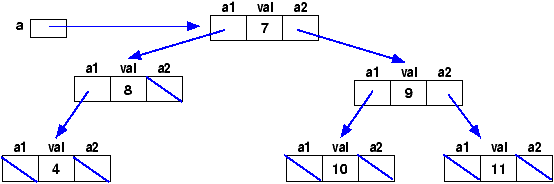
Arbres binaires (1/2)

class Arbre { int val; Arbre a1, a2; Arbre (int v, Arbre a, Arbre b) {val = v; a1 = a; a2 = b; } Arbre (int v) {val = v; a1 = null; a2 = null; }}

Arbre a = new Arbre (7, new Arbre (8, new Arbre(4), null), new Arbre (9, new Arbre(10), new Arbre (11)));

Planche 6

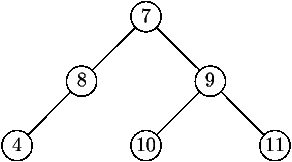
Arbres binaires (2/2)

ou encore plus abstraitement

Planche 7

Surcharge -- Overloading

Les fonctions (et les constructeurs) peuvent être surchargées.
Surcharge (Java) ¹ polymorphisme (ML)
- ·Une fonction polymorphe est la même pour une collection de types de ses arguments. Exemple: l'image mirroir d'une liste (sans préciser le type de ses éléments).
- ·Une fonction surchargée change de sens selon le type de ses arguments.
Les deux notions sont statiques. Elles n'interviennent qu'à la phase de compilation (et non à l'exécution).

Les principes des langages de programmation modernes sont enseignés en majeure 1.

Planche 8

Termes (1/3)

But: calculer. Les termes sont représentés par des arbres. Par exemple:

class Terme { final static int ADD = 0, SUB = 1, MUL = 2, DIV = 3, MINUS = 4, VAR = 5, CONST = 6; int nature; Terme a1, a2; String nom; int val; Terme (int t, Terme a) {nature = t; a1 = a; } Terme (int t, Terme a, Terme b) {nature = t; a1 = a; a2 = b; } Terme (String s) {nature = VAR; nom = s; } Terme (int v) {nature = CONST; val = v; }}

Planche 9

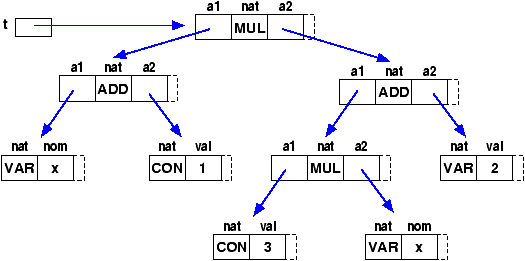
Termes (2/3)

Terme t = new Terme (MUL, new Terme (ADD, new Terme ("x"), new Terme (1)), new Terme (ADD, new Terme (MUL, new Terme (3), new Terme ("x")), new Terme (2)));

On a choisi ici de faire l'union de tous les champs. Seuls les plus significatifs figurent sur cette figure. D'autres représentations seront vues plus tard.

Planche 10

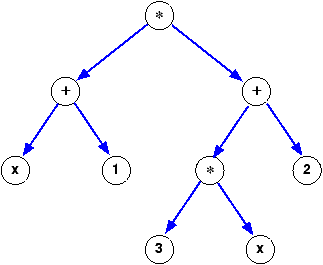
Termes (3/3)

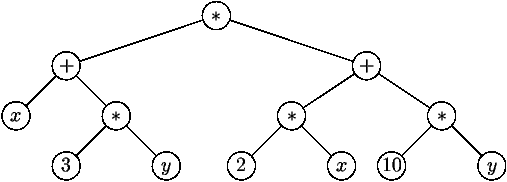
ou encore pour (x+1)*(3*x+2)

Exercice 1 Dessiner les ASA pour les termes x+y+z, x*y*z, x*y+z, x*(y+z), (a+a*a)*(a*a+a*a).

Planche 11

Grammaires formelles (1/4)

On fait appel aux grammaires algébriques (context-free).

G = (S, V, S, P) où

S		alphabet terminal
V		ensemble fini des variables non terminales (V Ç S = Ø)
S		axiome (S Î V)
P		ensemble fini de règles de productions X_i ® w_i (X_i Î V, w_i Î (S È V)^*)

Langage reconnu par G

· v ® v' implique uvw ® uv'w
· u ®^* v ssi u=u₀ ® u₁ ® u₂ ® ··· u_n=v (n ³ 0)
· L(G) = { w | S ®^* w, w Î S^* }

Planche 12

Grammaires formelles (2/4)

Langage parenthésé

S={a, b }, V = { S }

S ® S S
S ® a S b
S ®

Représentation linéaire d'arbres

S={[, ], nb } , V = { A }

A ® `[` A nb A `]`
A ®

Expressions arithmétiques 1

S={(, ), +, -, *, /, id, nb } , V = { E }

E ® E `+` E		E ® E `-` E		E ® E `*` E		E ® E `/` E
E ® id		E ® nb		E ® `(` E `)`

Expressions arithmétiques 2

S={(, ), +, -, *, /, id, nb } , V = { E, P, F }, E axiome

E ® P `+` E	E ® P `-` E	E ® P
P ® F `*` P	P ® F `/` P	P ® F
F ® id	F ® nb	F ® `(` E `)`

Planche 13

Grammaires formelles (3/4)

Langage parenthésé

S={a, b }, V = { S }

S ® S S
S ® a S b
S ®

® S S ® S aSb ® S aSSb ® S aSb ® S aaSbb ® S aabb ® aSbaabb ® abaabb

S		® aSb ® aS Sb ® aSSSb ® aSaSbSb ® aSaSSbSb ® aaSbaSSbSb ® aaaSbbaSSbSb
		® aaaSbbaSSbaSbb ® aaabbaSSbaSbb ® aaabbaSbaSbb ® aaabbabaSbb ® aaabbababb

a correspond à parenthèse ouvrante '(',
b correspond à parenthèse fermante ')'.

Planche 14

Grammaires formelles (4/4)

Représentation linéaire des arbres binaires

S={[, ], nb } , V = { A }

A ® `[` A nb A `]`
A ®

A		®`[` A 7 A`]` ®`[[` A 8 A`]` 7 A`]` ®`[[[` A4A`]` 8A`]` 7A`]` ®`[[[` 4A`]` 8A`]` 7A`]`
		®`[[[` 4`]` 8A`]` 7A`]` ®`[[[` 4`]` 8`]` 7A`]` ®`[[[` 4`]` 8`]` 7`[` A9A`]]`
		®`[[[` 4`]` 8`]` 7`[[` A10A`]` 9A`]]` ®`[[[` 4`]` 8`]` 7`[[` 10A`]` 9A`]]`
		®`[[[` 4`]` 8`]` 7`[[` 10`]` 9A`]]` ®`[[[` 4`]` 8`]` 7`[[` 10`]` 9`[` A11A`]]]`
		®`[[[` 4`]` 8`]` 7`[[` 10`]` 9`[` 11A`]]]` ®`[[[` 4`]` 8`]` 7`[[` 10`]` 9`[` 11`]]]`

Long mais précis !
On peut abstraire les dérivations par un arbre de dérivations ou encore arbre syntaxique.

Planche 15

Arbre syntaxique (1/5)

mot [[[4]8]7[[10]9[11]]]

grammaire

A ® [ A nb A ] A ®

	arbre syntaxique
	(arbre de syntaxe
	concrète)

	arbre de syntaxe
	abstraite

Planche 16

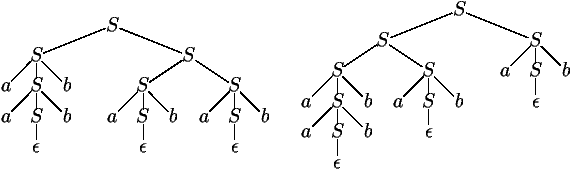
Arbre syntaxique (2/5)

Mot aabbabab Grammaire

S ® S S

S ® a S b

S ®

etc.

Langage parenthésé

Une grammaire est ambigue si elle génère plus d'un arbre syntaxique pour un même mot reconnu.

Exercice 2 Trouver une grammaire non ambigue générant le langage parenthésé précédent.

Planche 17

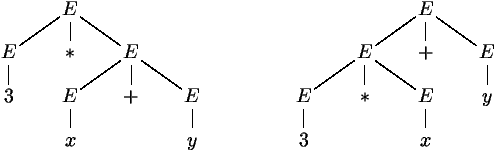
Arbre syntaxique (3/5)

Mot 3*x+y Grammaire Expressions arithmétiques 1

Grammaire ambigue, car deux arbres syntaxiques pour 3*x+y

Þ deux ASAs pour 3*x+y

Planche 18

Arbre syntaxique (4/5)

Mot (x+3*y)*(2*x+10*y)Expressions arithmétiques 2

E ® P `+` E		E ® P `-` E		E ® P		P ® F `*` P		P ® F `/` P
P ® F		F ® id		F ® nb		F ® `(` E `)`

Planche 19

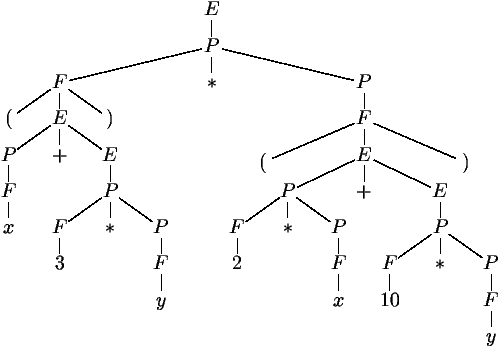
Arbre syntaxique (5/5)

ASA associé à (x+3*y)*(2*x+10*y)

Exercice 3 Dans les quatre grammaires précédentes, donner les grammaires non ambigues. Démontrer le!

Planche 20

Grammaires BNF (Backus-Naur Form) (1/2)

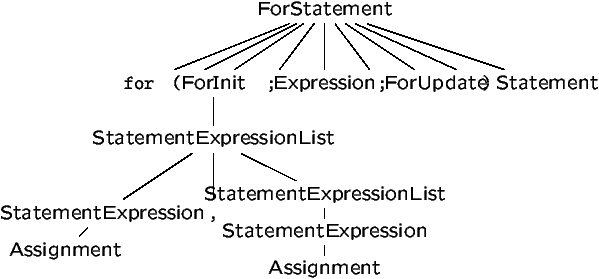
La syntaxe des langages de programmation est aussi décrite par une grammaire formelle. Les nombreuses variables non-terminales sont décrites par des identificateurs. Il y a souvent des raccourcis pour simplifier la notation. Un bout de la BNF de Java:


ForStatement:
        for ( ForInit_opt ; Expression_opt ; ForUpdate_opt )
                Statement

ForInit:
        StatementExpressionList
        LocalVariableDeclaration

ForUpdate:
        StatementExpressionList

StatementExpressionList:
        StatementExpression
        StatementExpressionList , StatementExpression

Planche 21


StatementExpression:
        Assignment
        PreIncrementExpression
        PreDecrementExpression
        PostIncrementExpression
        PostDecrementExpression
        MethodInvocation
        ClassInstanceCreationExpression

AssignmentExpression:
        ConditionalExpression
        Assignment

Assignment:
        LeftHandSide AssignmentOperator AssignmentExpression

LeftHandSide:
        Name
        FieldAccess
        ArrayAccess

AssignmentOperator:  one of
        = *= /= %= += -= <<= >>= >>>= &= ^= |=

Planche 22

Grammaires BNF (Backus-Naur Form) (2/2)

for (x = 1, y = 3; x < 100; ++x, ++y) { Statement}

Parfois, on écrit les BNFs avec des diagrammes en chemin de fer.

Planche 23

Analyse syntaxique

Donnés: grammaire G et un mot w
But: w Î L(G) ? Si oui, construire l'ASA de w.

2 grandes méthodes:

analyse descendante. On part de S pour atteindre w.
analyse ascendante. On part de w pour atteindre S.

déterministes (sans backtracking) pour des grammaires spéciales:

grammaires LL(k) pour analyse descendante
javacc ou Pascal [Wirth, 71]
grammaires LR(k) pour analyse ascendante
yacc [S. Johnson, 73]

Ici on verra l'analyse récursive descendante pour les grammaires LL(1).

Planche 24

Méthode récursive descendante (1/4)

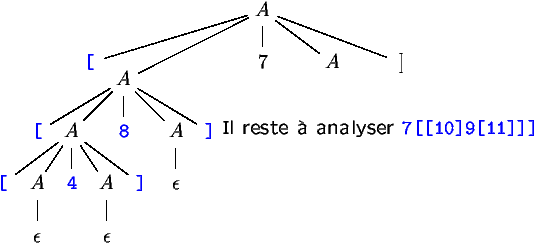
Mot [[[4]8]7[[10]9[11]]]

On part de l'axiome A en choisissant l'une des 2 règles de production en fonction du premier lexème (terminal) de la chaîne d'entrée.

A la fin, on obtient l'arbre syntaxique de la planche ??. 1

ireArbrexpressionroduitacteuraleurDeystemutrintrintlneriverrintlnrintlnrintln

Planche 25

Méthode récursive descendante (2/4)

Le lexème courant dans la variable globale lc.

static Lexeme lc;static void avancer() {lc = Lexeme.suivant(); }static Arbre lireArbre () { if (lc.nature == Lexeme.L_CroG) { avancer(); Arbre a = lireArbre(); if (lc.nature == Lexeme.L_Nombre) { int x = lc.val; avancer(); Arbre b = lireArbre(); if (lc.nature == Lexeme.L_CroD) { avancer(); return new Arbre (x, a, b); } else throw new Error ("Erreur de syntaxe. Il manque \"]\"."); } else throw new Error ("Erreur de syntaxe. Il manque un nombre."); else return null; }}

Planche 26

Méthode récursive descendante (3/4)

Le lexème courant dans la variable globale lc.

static Lexeme lc;static void avancer() {lc = Lexeme.suivant(); }static Terme expression() { Terme t = produit(); switch (lc.nature) { case Lexeme.L_Plus: avancer(); return new Terme (ADD, t, expression()); case Lexeme.L_Moins: avancer(); return new Terme (MINUS, t, expression()); default: return t; }}

Une fonction (récursive) par variable non terminale.
Au début, on appelle la fonction correspondant à l'axiome.

Planche 27

Méthode récursive descendante (4/4)

static Terme produit() { Terme t = facteur(); switch (lc.nature) { case Lexeme.L_Mul: avancer(); return new Terme (MUL, t, produit()); case Lexeme.L_Div: avancer(); return new Terme (DIV, t, produit()); default: return t; }}static Terme facteur() { Terme t; switch (lc.nature) { case Lexeme.L_ParG: avancer(); t = expression(); if (lc.nature != Lexeme.L_ParD) throw new Error ("Il manque ')'"); break; case Lexeme.L_Nombre: t = new Terme (lc.val); break; case Lexeme.L_Id: t = new Terme (lc.nom); break; default: throw new Error ("Erreur de syntaxe"); } avancer(); return t;}

On décide toujours avec pas plus d'un caractère d'avance LL(1).

Planche 28

Opérations sur les ASAs

belle impression (pretty-print), i.e. sans parenthèses superflues.
interprétation (évaluation d'expressions arithmétiques ou booléennes)
calcul formel (dérivation formelle, intégration, etc.)
compilation (génération de code)
transformations (passer en notation polonaise postfixe ou préfixe).
analyses statiques (vérifier l'absence de débordements flottants dans le logiciel embarqué d'Ariane 5 avant son exécution)

Planche 29

Evaluation d'expressions arithmétiques

Données: t terme, e table des valeurs des variables.
But: calcul la valeur du terme t dans l'environnement e.

static int evaluer(Terme t, Environnement e) { switch (t.nature) { case ADD: return evaluer(t.a1, e) + evaluer(t.a2, e); case SUB: return evaluer(t.a1, e) - evaluer(t.a2, e); case MUL: return evaluer(t.a1, e) * evaluer(t.a2, e); case DIV: return evaluer(t.a1, e) / evaluer(t.a2, e); case CONST: return t.val; case VAR: return valeurDe(t.nom, e); default: throw new Error ("Erreur dans evaluation"); }}static int valeurDe(String s, Environnement e) { if (e == null) throw new Error ("Variable non définie"); if (e.nom.equals(s)) return e.val; else return valeurDe(s, e.suivant);}

Planche 30

Dérivation

Données: t terme, x nom de variable.
But: calcul la dérivée du terme t par rapport à x.

static int deriver(Terme t, String x) { switch (t.nature) { case ADD: return new Terme(ADD, deriver(t.a1, x), deriver(t.a2, x)); case SUB: return new Terme(SUB, deriver(t.a1, x), deriver(t.a2, x)); case MUL: return new Terme(ADD, new Terme(MUL, deriver(t.a1, x), t.a2), new Terme(MUL, t.a1, deriver(t.a2, x))); case DIV: return new Terme(DIV, new Terme(SUB, new Terme(MUL, deriver(t.a1, x), t.a2), new Terme(MUL, t.a1, deriver(t.a2, x))), new Terme(MUL, t.a2, t.a2); case CONST: return new Terme(CONST, 0); case VAR: if (t.nom.equals (x)) return new Terme(CONST, 1) else return new Terme(CONST, 0); }}

Remarque: le résultat peut être un dag (dû au partage de sous-termes)

Planche 31

Belle impression

static void impExp (Terme t) { switch (t.nature) { case ADD: impProd(t.a1); System.out.print("+"); impExp(t.a2); break; case SUB: impProd(t.a1); System.out.print("-"); impExp(t.a2); break; default: impProd(t); }}static void impProd (Terme t) { switch (t.nature) { case MUL: impFact(t.a1); System.out.print("*"); impProd(t.a2); break; case DIV: impFact(t.a1); System.out.print("/"); impProd(t.a2); break; default: impFact(t); }}static void impFact (Terme t) { switch (t.nature) { case CONST: System.out.print(t.val); break; case VAR: System.out.print(t.nom); break; default: System.out.print("("); impExp(t); System.out.print(")"); break; }}

Belle symétrie par rapport à l'analyse syntaxique (opération inverse).

Planche 32

Opérateurs non associatifs

La méthode récursive descendante parenthèse mal les opérateurs non associatifs.

x+y+z	analysé comme	x+(y+z)
x-y-z		x-(y-z)

Pour revenir au parenthésage naturel, implicitement à gauche, il faut transformer la grammaire en:

E ® E `+` P	E ® E `-` P	E ® P
P ® P `*` F	P ® P `/` F	P ® F
F ® id	F ® nb	F ® `(` E `)`

Impossible à analyser en récursif descendant (récursivité gauche dans la grammaire), puisque E ®^* Eu.

Avec des expressions régulières, on écrit la grammaire comme

E ® P (`+` P)^*	E ® P (`-` P)^*
P ® F (`` F)^	P ® P (`/` F)^*
F ® id	F ® nb	F ® `(` E `)`

et on utilise un while dans la programmation.

Planche 33

Analyse syntaxique

théorie des langages formels [Chomsky, Schutzenberger, 1960]
analyse syntaxique [Aho, Sethi, Ullman, 1980]
compilation [Appel], [Caml, Ocaml, ...Leroy]
analyse de langues naturelles

Les grammaires formelles Þ Automates et Calculabilité en majeure M1;
les analyseurs syntaxiques Þ Compilation en majeure M2.

Planche 34

Exercices

Exercice 4 Programmer la belle impression.

Exercice 5 Essayer d'imaginer ce que pourrait être l'analyse ascendante.

Exercice 6 Trouver une solution grammaticale LL(1) pour l'analyse syntaxique des opérateurs non associatifs.

Exercice 7 Donner des exemples où l'analyse descendante a des difficultés, mais pas une analyse ascendante.

Exercice 8 Faire une calculette logique

Exercice 9 Faire une calculette Texas Instrument (sans notation polonaise).

This document was translated from L^AT_EX by H^EV^EA.